When my colleagues asked ME to call 2 of my favorite product for my birthday sale, I didn’t hesitate. Yes,
Continue reading »

When my colleagues asked ME to call 2 of my favorite product for my birthday sale, I didn’t hesitate. Yes,
Continue reading »
The end of the year is springing up quick. nowadays is that the day we’re cathartic the last update of
Continue reading »
You might have noticed: Google has created search results snippets longer. within the past it showed up to ~160 characters,
Continue reading »
A year perpetually sounds like such a protracted time. however whenever we tend to reach the tip of 1, we
Continue reading »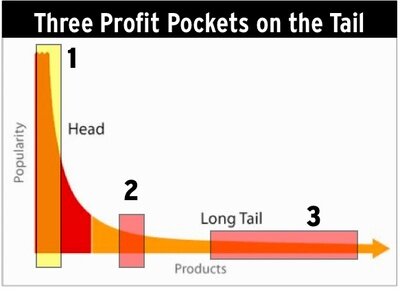
Focusing on long tail keywords may be a nice SEO-tactic for blogs. a protracted tail keyword strategy makes it straightforward
Continue reading »
Writing a web log post, like all different writing, is a skill. to stay your reader interested, you must suppose
Continue reading »
Now, the reality is, thusme ranking puzzles ar so complicated, they’ll solely be solved by a proper competitive audit. however
Continue reading »
Success is not associate degree nightlong development once it involves SEO, however with the correct method and a dose of
Continue reading »